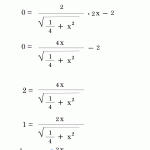
分数関数は関数同士の商で表されるので、商の微分公式で微分できます。 商の微分公式 \(\displaystyle y = \frac{f(x)}{g(x)}\) の導関数は、全微分 関数 f(x, y) が x0, y0 で全微分可能であれば,この点での接平面の方程式は z − f(x0, y0) = fx(x0, y0)(x − x0) fy(x0, y0)(y − y0) で表されます。 x − x0 = dx , y − y0 = dy , z − f(x0, y0) = dz と座標変換し, fx(x0, y0) と fy(x0, y0) をそれぞれ fx(x, y) と fy(x, y) に 今回は無理関数や分数関数の微分について解説していきます。 まずは n 次関数の形に式変形をして微分していきましょう。 教科書より詳しい高校数学

ミクロ経済の微分 高校生の頃数学をあまりやらなかったのでミクロ経済を習っ Okwave
分数の微分 ルート
分数の微分 ルート-21 分数阶微积分的历史 分数阶微积分已有300多年的历史,最早由L'Hospital 1695年9月30号在给Leibnitz的信件中提出,经Euler,Lagrange,Lacroix,Fourier,Liouville,Riemman,Weyl 等数学家的辛勤工作初步建立起来的,但数学理论仍有诸多不完善。問題点 分数階微分についての理解が足りていないのでテストケースが用意できていません。 \(0 < \alpha < 1\) の範囲を超えると計算結果がおかしいように見えます。 積分方向は見当違いの値がでているようにしか見えません。




Ai 機械学習の数学 偏微分の基本 意味と計算方法 を理解する Ai 機械学習の数学入門 It
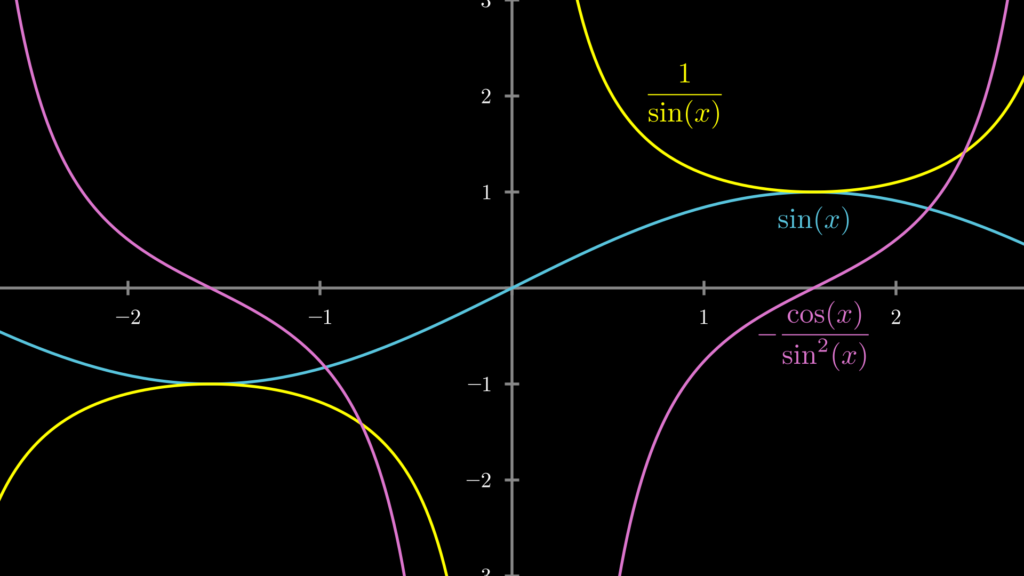
分数 微分学是描述非线性问题的方法和手段,研究 分数微积分 学有着重要的意义。 本 薛定宇教授的 分数阶 simulink工具箱,包含 分数阶 变换, 分数阶 PID控制, 分数阶 矩阵等模块,用于 分数阶 系统仿真。 使用方法: 1 )解压,并在matlab下导入路径;2)在微分の公式一覧 このページでは、関数 f (x) f ( x) を 微分 して得られる導関数 f ′(x) f ′ ( x) の基本的な公式を掲載しています。 また、 和や差、積、商の微分公式や合成関数の微分公式なども掲載しています。 導出方法はみなさん自身でご確認の上当ページでは、これを「分数の微分公式」と呼ぶことにします。 分数の微分公式 { 1 f (x) }′ = − f ′(x) {f (x)}2 { 1 f ( x) } ′ = − f ′ ( x) { f ( x) } 2 例えば、 f (x) = sin(x) f ( x) = sin ( x) としたら次のようになります。 { 1 sin(x) }′ = − sin(x)′ {sin(x)}2 = − cos(x) sin2(x) { 1 sin ( x) } ′ = − s i n ( x) ′ { sin
偏導関数の定義より, x を定数とみなして y で微分する. 分数関数の微分の公式を用いる. = (9 x 6 y) − (10 x 6 y) (3 x 2 y) 2 = − x (3 x 2 y) 2分数を求める 線形方程式 二次方程式 不等式 方程式のシステム 行列 三角法 簡約する 評価 グラフ 方程式を解く 微 頭の中では、「yの微分」と読んでいた方がよいのですが、 発音するときは、「ディーワイディーエックス」と読みます。 結論からいいますと、dy/dx は分数ではありません。 なぜなら、もし分数とするなら、 dxやdyの定義が必要になります。
対する分数階微分項が含まれることが分かったこ の ような分数階微分方程式を解く適切な数値積分アルゴ リズムは今のところ見当たらない Padvan(3)は 分数階微分項を含む線形の有限要素運 動方程式の数値積分法を開発しており,陰的解法,陽H) g (x +この主要部分を微分とよび,dyとしたのです。したがって、 です。ところで、x=xという式は常に成り立っています。したがって、この式をxで微分すると となり、 となるのです。 さて、分数を使わずに微分可能を表現できました。



絵で解いてわかる 逆三角関数 の微分 ばたぱら




お薦めの分数関数の微分法 Den Of Hardworking
上述の微分係数の定義に現れる分数 () は差分商とよばれる。これは関数 f(x) のグラフ上の2点 (a, f(a)) と (a h, f(a h)) を通る直線(割線という)の傾きを表している。H) g (x) h = lim h → 0 {1 g (x + 分数階微積分学 分数階微分作用素 このような理論の存在については、12年からのリウヴィルの論文にその素地を見ることができる23。函数の階数 a の分数階微分は今日ではしばしば




Ai 機械学習の数学 偏微分の基本 意味と計算方法 を理解する Ai 機械学習の数学入門 It




微分の疑問 添付画像の微分の解き方を教えてほしいです 分数だとやり 数学 教えて Goo
一般的な公式: ( x α) ′ = α x α − 1 で α = 1 2 とすればOKです。 ~証明2~ 微分の定義より、 ( x) ′ = lim h → 0 x h − x h です。 この分母分子に ( x h x) をかけて分子を有理化すると、 lim h → 0 h h ( x h x) となります。 h → 0 で x h → x となるので上式は 1 2 x となります。 関連: 分子の有理化と極限の問題 ちなみに、三乗根以上については 三乗根、累乗根12.7.29 分かりやすい微分・積分について 永井建哉 参考)リンク先 素数分布の研究 微分・積分と聞くだけで苦手意識のアレルギーの人もいるだろうし、あるいはそれ以前に聞きなれない言葉だと思う人がいるかもしれない。 指数部分が分数になっている微分式を 見た途端に頭のごちゃごちゃになっていたみたいです。 分数でも整数と同じように処理すれば いいことが分かりました。 助かりました。




大人になったら使わないのに なぜ私たちは 分数 を学ぶのか 分数 学ぶ 微分積分




部分分数分解を伴うラプラス変換について Webty Staff Blog
即积分算子a D n x 可以看作是整数阶导数算子的左逆 但反之不成立 事实上, 我们有下面的结 论 引理11 设f(x) 2 Cna;b,则 a D n x (D n f(x)) = f(x) n∑ 1 k=0 (x a)k k!分数関数の微分 II (関数の商の導関数) {h (x) g (x)} ′ = h ′ (x) g (x) − h (x) g ′ (x) {g (x)} 2 すなわち, f (x) = h (x) g (x) → f ′ (x) = h ′ (x) g (x) − h (x) g ′ (x) {g (x)} 2 導出 f ′ (x) = lim h → 0 f (x + 分数の微分について教えてください。 (2x1/2乗2)(x4乗2x1)を微分したら答えはどうなるのでしょうか?? (乗と分数の打ち方が分からなくて申し訳ありません) 答えも途中式もない資料なので、正解がわかりません。



微分 の 記号



平方根の微分 優技録
分数冪微分入門 横浜市立大学・国際総合科学部藤井一幸(FUJII Kazuyuki) International College of Arts and Sciences Yokohama City University 概要 このノートで分数冪微分(fractional derivatives) の超入門を行う。 I はじめに 関数を1回微分する、2回微分する、···と微積分の講義関数\(f(x)\)の導関数\(f'(x)\)は、次のように求めることができます。 $$f'(x)=\lim_{ h \to 0 }\frac{f(xh)f(x)}{h}$$ このように導関数を求めることを微分するといいます。 導関数の定義に従って微分をすると以下のようになります。 次の関数を微分しなさい。 $$f(x)=2x^2$$ $$\begin{eqnarray}f'(x)&=&\lim_{ h \to 0 }\frac{f(xh)f(x)}{h} \\5pt&=&\lim_{ h \to 0A < x < b 下面讨论n 重变上限积分a D n



高校数学 商の微分公式について分数の微分のとき 商の微分公式を使う時と 係数 Yahoo 知恵袋




分数関数の積分 数学の偏差値を上げて合格を目指す
H) g (x) · 分数階微積分学 この文脈における「冪」の語は作用素の合成を繰り返し行うという意味で用いており、それに従えばたとえば f2 ( x) = f ( f ( x )) ということになる。 さてたとえば、 微分作用素 D の 平方根 (あるいは微分を半分だけ作用させる)という意味微分とは何か? - 中学生でも分かる微分のイメージ 微分の公式一覧 対数関数 log x の微分公式とその証明 偏微分の意味とやり方 部分積分の公式とその証明方法、使い方のコツ 部分積分を使う積分計算の解き方 例題と解説




微分係数の極限値を求める時に分数の形ではカッコをつけないのにlim A B などの形 Clear




分数関数の最小値 高校数学 入試問題 大好きな問題たち Youtube
H) g (x) − h (x) g (x + 微分(導関数)の定義式 関数 f(x) に対して、導関数 f ′ (x) は以下の式で定義される ● f ′ (x) = lim h → 0 f(x h) − f(x) h分数階微分の謎 線形代数、分数階微分、シュレディンガー方程式の三題話 分数階微分? InterLabの1999No5を読んでいると面白い記事があった。いわき明星大学理工学部の榊原教授の「Waveletと数式処理ツール」という記事である。




タンジェントの微分を忘れた時は 数学の星



分数関数の微分のやり方 商の微分公式 を誰でもわかるように解説 Headboost
H) g (x +マイナス乗の微分 例3:f(x) = 1 x2 f(x) = 1 x2 = x−2 ···指数表記 ∴ f′(x) = ¡ x−2 ¢′ = −2x−3 ···微分公式 = − 2 x3 ···分数表記(できればここまで:中学生でも意味がわかるので) 問2 上の例にならって、次の関数を微分しなさい。 1 f(x) = 1 x4 = ←ここに指数表記をつづけて書く(小問2高校数学Ⅲで習う商の微分法,分数関数の微分法について,解説と問題です.画面上で採点できます. 商,分数関数の微分 → 携帯版は別頁



1
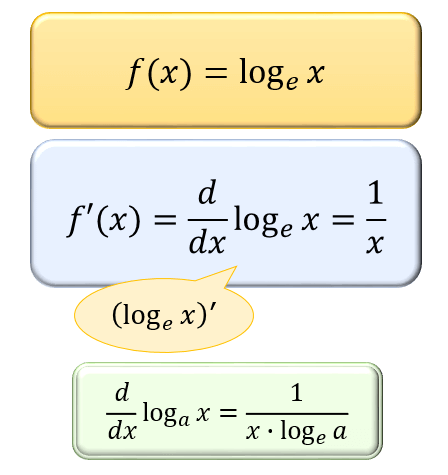



自然対数 Log X の微分公式について 導関数の定義式と意味から分かる証明方法 アタリマエ
x^nをxで微分するとnx^ (n1)になるというのは習ったと思いますが、 それを利用します (ちなみに記号^は累乗の記号です。 a^bは「aのb乗」を意味します)。 8/x = 8x^ (1)と変形して、無理矢理x^nの形に直します。 x^nをxで微分するとnx^ (n1)になるので、 x^ (1)をxで微分するとx^ (2)となります。 よって8x^ (1)をxで微分すると8x^ (2) = 8/ (x^2)となります。 43 分数阶微分,GrumwaldLetnikov定义在图像的数值实现中更为准确:Gamma函数:若s(t)的持续期t a,t,将函数持续期间a,t按单位间隔h=1进行等分,得到:推到一元函数是s(t)的 v 阶分数阶微分差分表达式为:这n个非零系数只有常数"1",其他都是n1个都是分数阶微分阶次的函数。H) − f (x) h = lim h → 0 h (x +



分数関数とは グラフや微分 積分 不等式の解き方 受験辞典




とと Pa Twitter 分数関数の微分 積の微分を認めたら簡単がち
分数阶微积分的应用——等时降落问题(Tautochrone problem) 等时降落问题示意图(维基百科) 等时降落问题,即找到一个曲线,使得物体放置在曲线中任意位置开始降落的时间均相同。 现在我们可以再将这个问题变成微分方程。 由于是曲线运动,直接使用H) − h (x) g (x) h = lim h → 0 h (x +商(分数)の微分法則 関数の分数の微分は以下の通りです。 分数の微分法則 { 1 f (x) }′ = − f ′(x) {f (x)}2 { 1 f ( x) } ′ = − f ′ ( x) { f ( x) } 2 商の微分法則 { g(x) f (x) }′ = g′(x)f (x)−f ′(x)g(x) {f (x)}2 { g ( x) f ( x) } ′ = g ′ ( x) f ( x) − f ′ ( x) g ( x) { f ( x) } 2



Kit Mathematics Navigation Translated By Google Translate
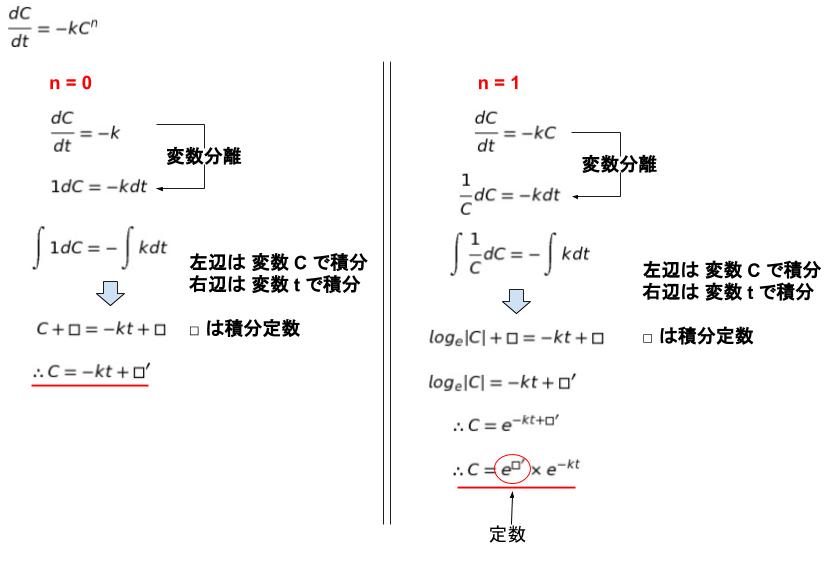



微分方程式 薬学 これでok
2 第一讲分数阶微分方程 易知,对任意正整数n,都有 Dn (a D n x f(x)) = f(x);分数階微分積分学 (ぶんすうかいびぶんせきぶんがく、 英 fractional calculus )は 解析学 (特に 微分積分学 )の一分野で、微分作用素 D および積分作用素 J が実数冪あるいは複素数冪をとる可能性について研究する 学問 である。 本来、 という微分の表記法は分数ではありませんが、右辺の を分数であるとみなし を約分すると、左辺の に一致するということがわかると思います。 つまり、 という微分の表記法は、計算上は分数のように扱って良いということになります。



数 微分法 数学用語解説




Log 微分 分数
分数は次の形を利用して微分していきましょう。 $$\left\{ \frac{f(x)}{g(x)}\right\}'=\frac{f'(x)g(x)f(x)g'(x)}{\{g(x)\}^2}$$ $$y'=\frac{(\sin x)'}{\sin^2 x}$$LaTeXコマンド 微分と偏微分のさまざまな記号(導関数に値を代入する記法など) 微分は f' (x) のように関数にダッシュをつけたり、df/dx のように分数で表したり、いろいろな記法がある。分数の偏微分 f(x、y)=1/(xy) x^2で偏微分せよという問題なのですが、 答えは 1/(2x^3y) になるようなのですが、そこまでの計算過程がイマイチ分かりません。 詳しい計算過程と高校、大学で習った※※を使う等、優しく教えて頂けないでしょうか?



3




合成関数の微分公式と例題7問 高校数学の美しい物語




部分分数分解を伴うラプラス変換について Webty Staff Blog




分数関数の微分について Den Of Hardworking




分数冪微分方程式と Discrete Delta Potential 幾何学的力学系の新展開




不定形の極限値をロピタルの定理で求める例 微分積分学 タロウ岩井の数学と英語 Note




微分 高階微分とマイナスの指数 大人が学び直す数学




部分分数分解の公式 ヘビサイドのカバーアップ法 Rpgツクールと数学のブログ




高校数学 X Pの微分公式 映像授業のtry It トライイット




Logの微分 例題を解説 分数 合成関数はどうやる 数スタ




分数阶微分方程的有限差分方法 Amazon Com Books




極限値を微分係数f A を用いて表す問題を解説 数スタ



分数の微分で質問です これの微分のやり方と答えを教えてください Yahoo 知恵袋




数学 の微分の問題です 4 の関数を微分する問題がわかりません 途 数学 教えて Goo




Logが入っている微分が全然わかりません Clear




ミクロ経済の微分 高校生の頃数学をあまりやらなかったのでミクロ経済を習っ Okwave




微分は Dy か Dy Dx か おにノート おーにしの物理 数学ノート




微分のやり方 計算方法まとめ 分数や三角関数のやり方は 数スタ




Y 2 X 2 1 を二階微分してください Clear
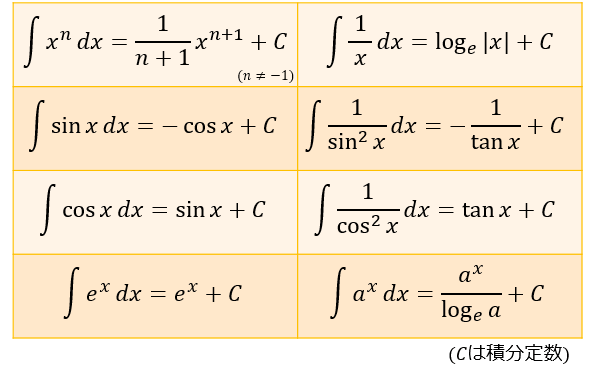



積分の公式一覧 アタリマエ




X微分




部分分数分解の公式 ヘビサイドのカバーアップ法 Rpgツクールと数学のブログ




微分法基礎 分数の微分 Youtube



微分公式 制御工学の基礎あれこれ




分数のように見なす 変数分離形の微分方程式 Youtube



分数の微分ってどうすればいいんですか この問題なんです 公式通りに Yahoo 知恵袋




高校数学 微分形接触型の一種 分子が分母の微分型 置換せずに瞬殺せよ 受験の月




Y X X分の2 を微分するという問題の解説が こうなるのはなぜですか Clear
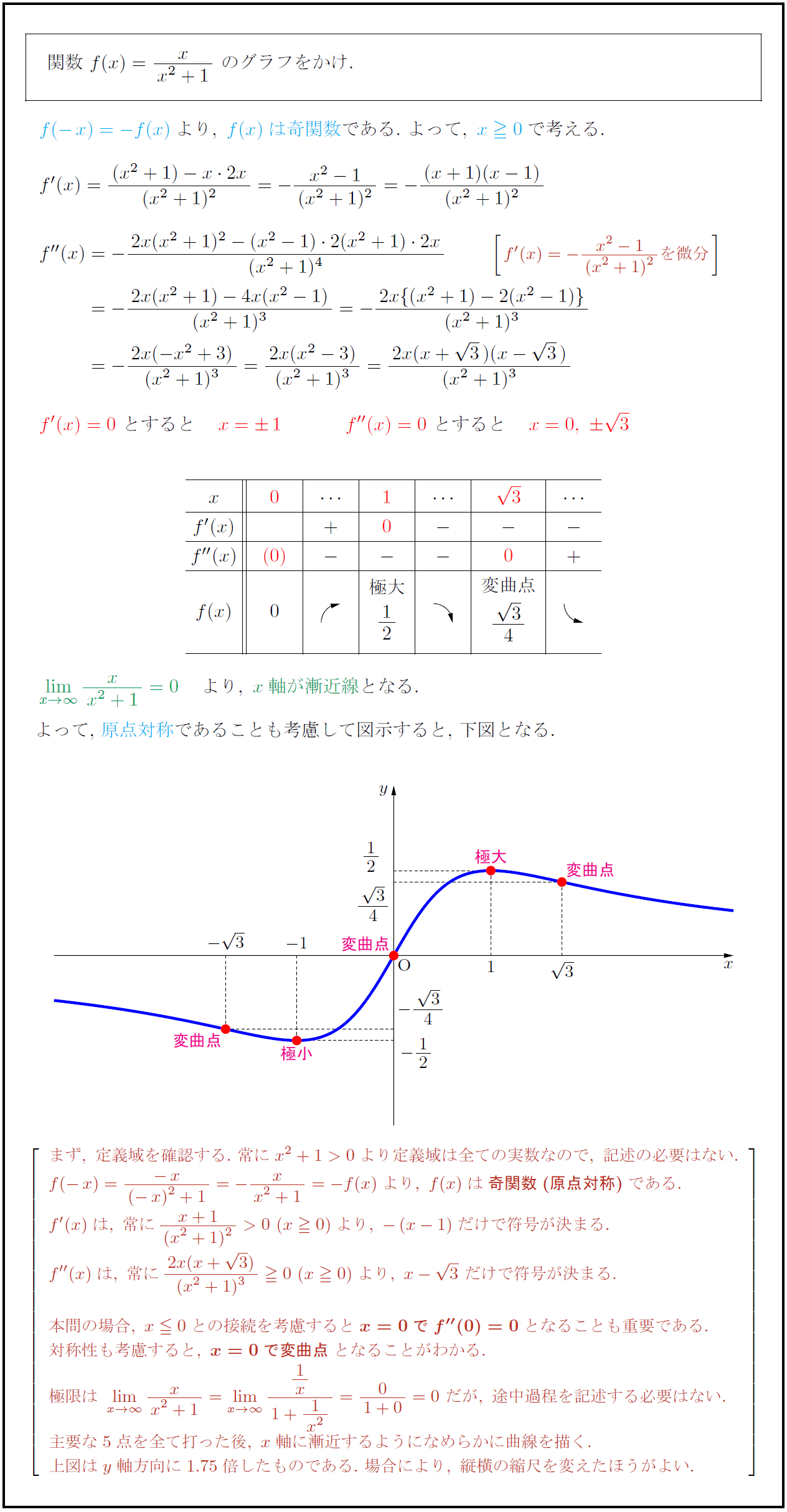



高校数学 分数関数 Y X X 1 のグラフ 受験の月




分数階微積分学 Wikipedia




うさぎでもわかる解析 高校数学 数3 Part05 部分分数分解を用いた積分 工業大学生ももやまのうさぎ塾
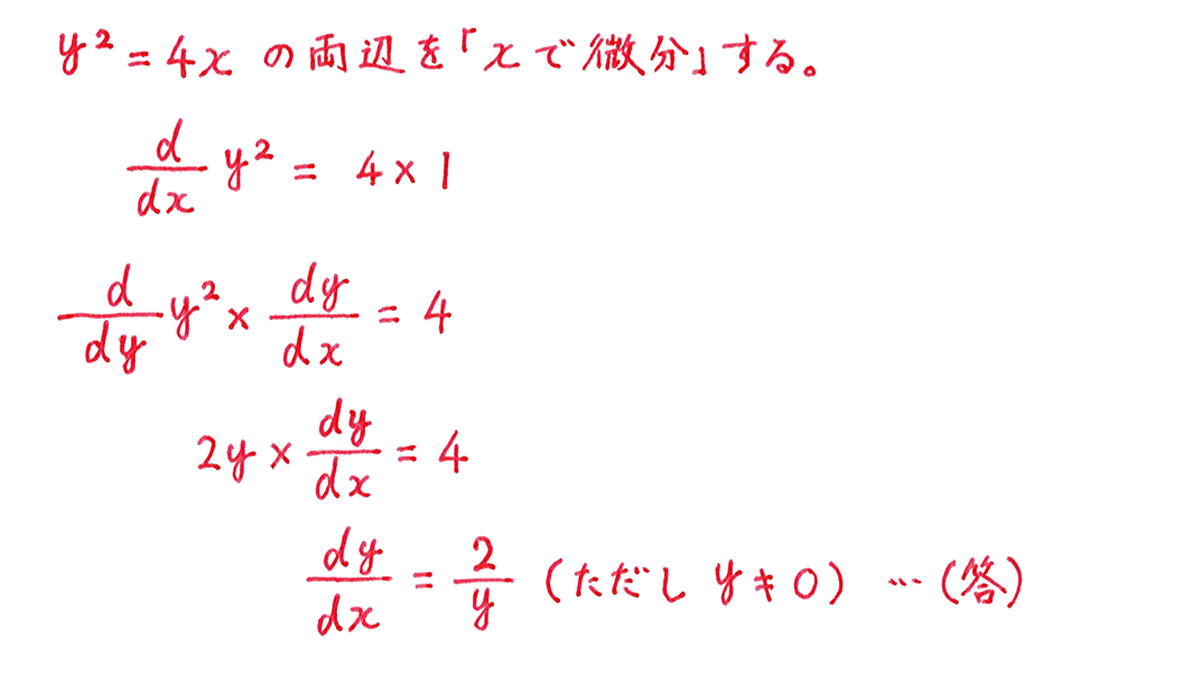



高校数学 D Dx D Dyについて 1 問題編 映像授業のtry It トライイット




Logの中身 真数 が分数のときの微分計算 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




微分積分とは 高校数学の基礎から応用までわかりやすい記事総まとめ




Ai 機械学習の数学 偏微分の基本 意味と計算方法 を理解する Ai 機械学習の数学入門 It
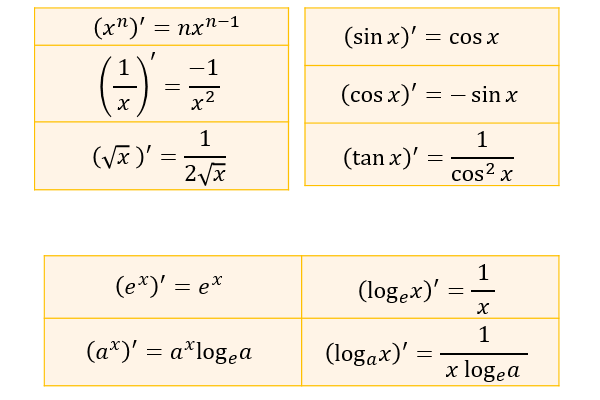



微分の公式一覧 アタリマエ




商の微分法則 Wikipedia




機能工学



微積分公式 京極一樹の数学塾




高校数学 関数の最大値 最小値 2 問題編 映像授業のtry It トライイット




分数の微分がわかりません やり方を教えてください Clear




微分の公式一覧とその証明が必ず理解できるようになる解説 Headboost
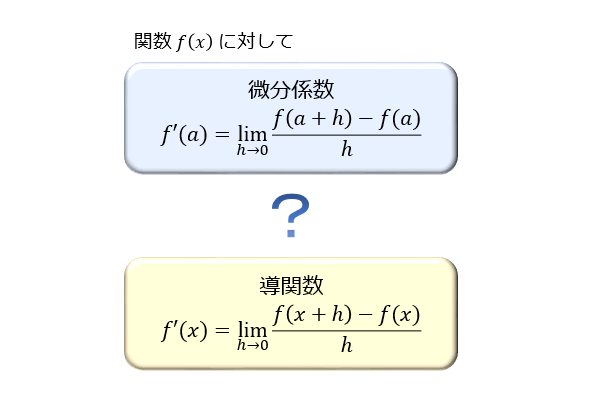



微分係数と導関数の違いとその使い分け アタリマエ



微積分公式 京極一樹の数学塾




三角関数の微分 公式の証明と例題 高校生向け受験応援メディア 受験のミカタ



3




分数階微積分とは何ですか




Logの中身 真数 が分数のときの微分計算 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



数学 この問題 分数の微分を教えて下さい Xについて Yahoo 知恵袋
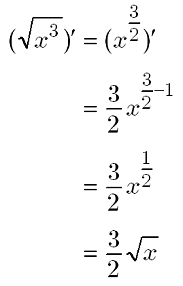



微分 羃乗関数の指数を拡張する 大人が学び直す数学



無理関数の導関数




平方根の微分 優技録




分数阶偏微分方程的动力学 黄建华 辛杰 沈天龙 Amazon Com Books
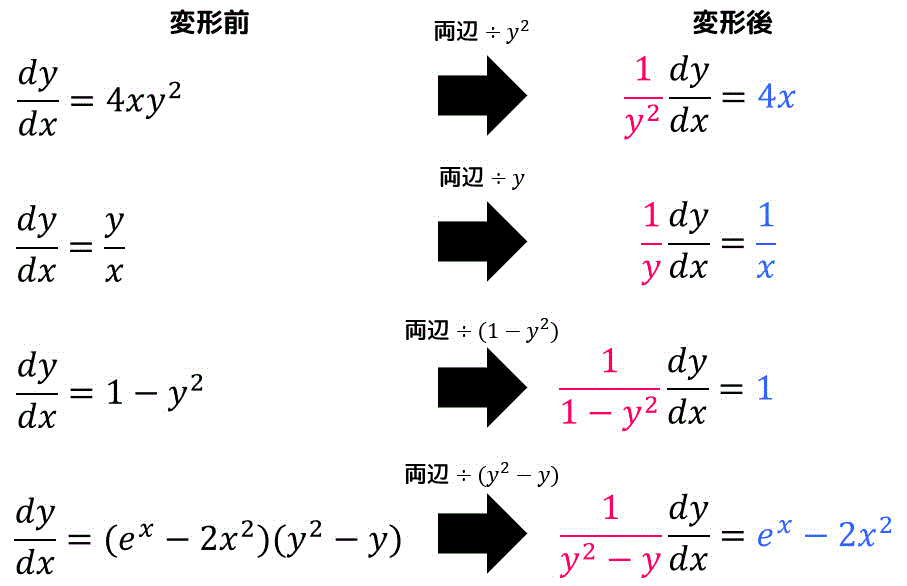



うさぎでもわかる微分方程式 Part01 変数分離形 1階微分方程式 工業大学生ももやまのうさぎ塾




分数関数の微分法 暗記をグッと減らせる 分数の微分が思考停止2秒で解ける 青春マスマティック
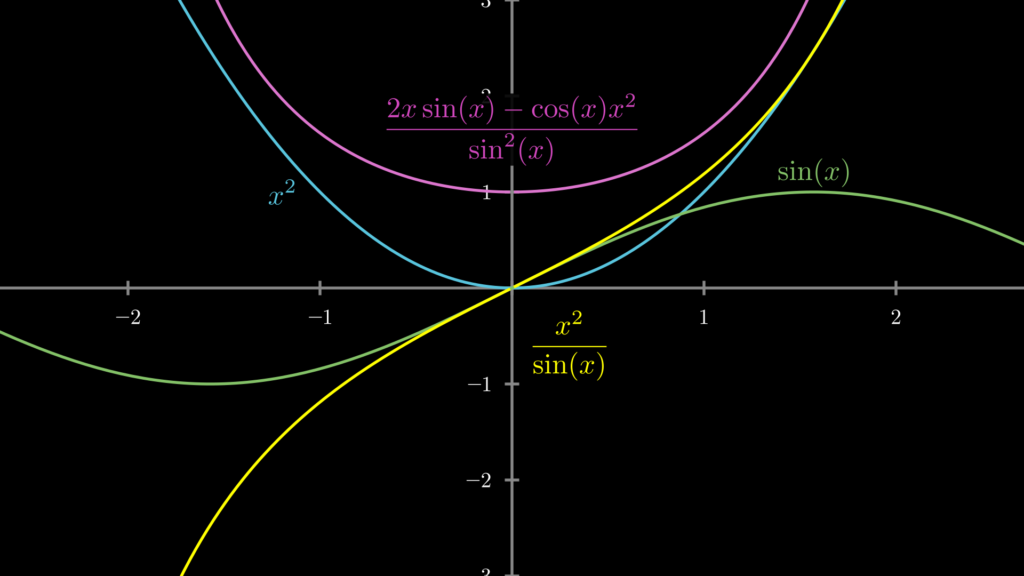



分数関数の微分のやり方 商の微分公式 を誰でもわかるように解説 Headboost
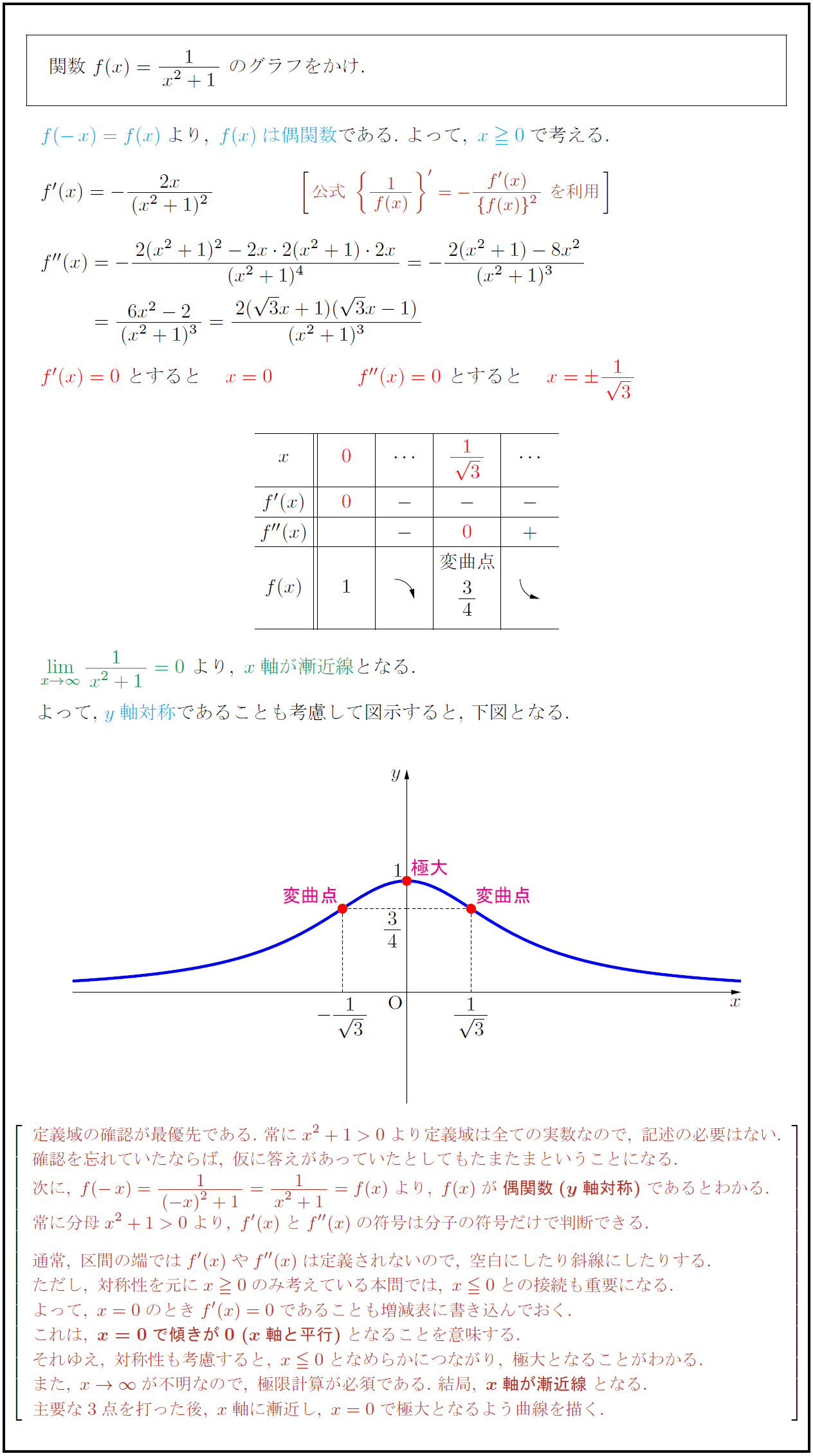



高校数学 分数関数 Y 1 X 1 のグラフ 受験の月



1




1変数関数微分 経済学メモ Atwiki アットウィキ




数学 For 大学受験 問題 Mathworld4 微分積分 数学iii T Co Q8z50aux96 Twitter




微分 分数関数の微分 大人が学び直す数学




導関数dy Dxのdyとdxを説明するのは実は苦労




高校数学 F X F X の不定積分 1 映像授業のtry It トライイット




部分分数分解と有理関数 三角関数 無理関数の不定積分




分数関数の微分について Den Of Hardworking



商 分数関数の微分




単純な方法で微分は誤差無しの分数とみなせる




商の微分公式で分母の2がなぜ二乗にならないのですか 初歩的なことかも 高校 教えて Goo




高校数学 陰関数の微分法 受験の月




みある ฅ W ฅ 5は分数関数f X G X の微分方程式 F X G X F X G X G X 2に入れて頑張る 8は なんだろう Sin 2xの微分が分からない感じですかね F G X F G X G X って公式使うとできます T Co Mntxypwgms




高校数学 D Dx D Dyについて 1 問題編 映像授業のtry It トライイット




七誌 Gm3d2 分数の微分をどうにか導きました 積の微分の応用まではすぐ思い付いたのですが 1 F が結構ややこしいですね T Co Z1ni4s1mss




うさぎでもわかる解析 高校数学 数3 Part05 部分分数分解を用いた積分 工業大学生ももやまのうさぎ塾




商の微分 公式と証明 覚え方も 高校数学の知識庫



この分数の微分はどうして分子だけしか微分しないんでしょうか Yahoo 知恵袋



分数関数の積分 高校数学 高校化学 高校物理に関連した基礎の基礎の復習です




下の式は上を微分したものですが分数がなぜそうなるのかが わかりません Clear




偏微分 数学について 四角で囲んだ数式はどのように算出されたのか 数学 教えて Goo




分数階微積分学 Wikipedia



商 分数関数の微分




Logの中身 真数 が分数のときの微分計算 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



分数の偏微分がわかりません 教えてください Yahoo 知恵袋



0 件のコメント:
コメントを投稿