2点間の距離の公式は,三平方の定理を使って示すことができる. で,2点 A (x1 , y1 ) , B (x2 , y2 ) 間の距離が求められる. ※ この公式は B の x 座標や y 座標が A の x 座標や y 座標よりも小さいときも成り立つ.(2乗するので,どちらの場合も正になる結論から言ってしまうと、 中学3年生で学習する三平方の定理 共円直交対角線四辺形の面積 k を四辺の長さで表す公式は、トレミーの定理と直交対角線四辺形の面積公式を組合わせることで直接的に得られる。それは = () というものである 。S= 1 × c × 4√ s(s-a)(s-b)(s-c) (←ルートを表す)

二次方程式の解き方 平方根の知識を使う問題のパターン 中学や高校の数学の計算問題
三平方の定理 公式 ルート
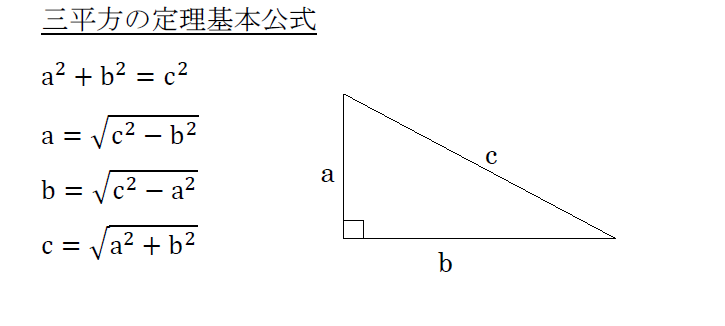
三平方の定理 公式 ルート- 三平方の定理とは 三平方の定理とは,直角三角形において各辺の関係は 斜辺 2 = 底辺 2 + 高さ 2 となる定理のことで、この定理のおかげで、 2辺の長さが分かればあと1辺の長さを求めることができる。三平方の定理とは? 三平方の定理とは、古代ギリシアの数学者である「ピタゴラス」の名前を取って、「ピタゴラスの定理」と呼ぶこともある定理で、「直角三角形の3辺の長さの関係」表す定理です。 直角三角形とは、中学数学で散々見てきた これですね。




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく
SNAPMAN 対角線長を計算する × 小数点以下 桁まで表示 答え **** 公式(三平方の定理) 対角線=√(底辺 2 +高さ 2 ) 電卓で計算する方法 例:2 これを√a二乗×b二乗で電卓たたけば対角線の長さが出てきます これは建物のカネ(直角)を確認する時も使っ三平方の定理とは、直角三角形の3辺の長さの関係を表す公式の事を言います。 また、別名「ピタゴラスの定理」とも呼ばれています。 この呼び方の方が有名でしょうか。 古代中国でもこの定理は使われていて、それが日本に伝わり、江戸時代には鉤股弦円周角の定理 円周角の定理 必須の問題10選を解説! 円周角の発展問題、円の中にブーメラン型! 三平方の定理 初めに覚えておきたい三平方の基本公式! 三平方の定理の逆ってなに?どうやって証明するの? 二点間の距離の求め方をイチから解説!
三平方の定理の最も変わった証明方法はなんですか? 既に回答があるように, 三平方の定理は数多く知られています。しかし, 三平方の定理があまりにも基本的な性質なので, 変わった証明を考えるのは困難です。変わったことをしようとすると, 実は三平方三平方の定理は、直角三角形の3つの辺の長さの関係を表わした定理で、直角三角形の直角を挟む2つの辺の長さをそれぞれ a a 、 b b とし、斜辺の長さを c c とすると、 a2 b2 = c2 a 2 b 2 = c 2 の関係が成り立つ、という定理です。ピタゴラスの定理(ピタゴラスのていり)は、直角三角形の3辺の長さの関係を表す等式である。三平方の定理(さんへいほうのていり)、勾股弦の定理(こうこげんのていり)とも呼ばれる。1 1 概要 2 ピタゴラス数 21 ピタゴラス数の性質 22 Jesmanowicz 予想 3 一般化 31 角の一般化 32 指数の
まとめ1(展開,因数分解,根号) まとめ2(2次方程式,解の公式,文字係数) まとめ3(三平方の定理,辺の比が分かっている三角形,空間図形) まとめ4(素数,最大公約数,最小公倍数,整数問題) まとめ5(平行線と線分の比,相似比) まとめ6(2次関数,変化の割合,放物線と直線) 三平方の定理とは、直角三角形において3辺の長さの関係を表す公式のことをいいます。 直角と隣り合う2辺の長さをそれぞれ a 、 b 、直角の向かい側にある最も長い辺 (斜辺)の長さが c となる直角三角形があるとします。三平方の定理を応用すると、正三角形の高さを求めることができる。 例題 右の図のような正三角形の高さ h を求めよ。 (解法) 正三角形 abc の頂点aから底辺bcに垂線ahをおろすと、図のように、点hはbcの中点になる。 なので、まずbhの長さは 1cm である。




中学数学 平方根のひみつ 都立高校入試で成功する方法




ピタゴラスの第2定理発見 三平方根の定理 直角三角形の菅数論の定理 発想力教育研究所 素数誕生のメカニズム
三平方の定理とは、直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを cとしたときに、公式 a 2 b 2 = c 2 が成り立つという定理です。 ここで、斜辺とは、直角三角形の直角に対する対辺のことです。 三平方の定理は、別名、ピタゴラスの定理とも呼ばれます。1 三平方の定理 三平方の定理の歴史や由来を知る §1.ピタゴラス以前のピタゴラスの定理(古代エジプトとは紀元前3000年~紀元前30年) 古代エジプトではナイル川の氾濫で土地の区画が 分からなくなることがたびたびあったそうです。 三平方の定理の証明⑩(無限等比級数を利用した証明) 年8月28日 中3数学 平面図形 中3数学 三平方の定理には数百もの証明方法があります。 今回は、直角三角形を無限に細かくしていき、最終的には無限等比級数を利用する証明方法を紹介します



日曜大工で使う数式



Sinaを求めるにあたって三平方の定理を使うのはわかるのですが そうする Yahoo 知恵袋
三平方の定理の特別三角形の1対1対ルート2と1対2対ルート3の意味がわからないので わかるかたは教えてください 高校 締切済 教えて!goo 単元 立体の体積と表面積, 「75°、15°、90°の辺の比など、教科書には載っていない便利な定理・公式です。 実際に高校受験のときによく使っていました。 覚えておくとかなり役に立ちます。」, 学年 中学3年生, キーワード 三平方の定理,相似な図形,円の接線,内接円,外接円,正三角形,正 辺の長さが2桁でも気にすんな。 三平方の定理(ピタゴラスの定理)の公式にぶち込めばいいんだ。 x² = 5² 12² x = 13 直角三角形と言えども、いつも右下に直角が来るとは限らんぞ。




Yasuhiro Abe A Personal Blog ルートを使わずにどうしろと



三角形の高さの計算の仕方を教えてください 中3の三平方の定理の利用とい Yahoo 知恵袋
例 (1) 1 2 x 斜辺がxなので 1222=x2 x2 = 5 x > 0 より x= 5 (2) x 12 13 斜辺が13なので x2122公式やルートの意味から平方根の近似値の覚え方、応用問題の解き方までカバーしているので、数学が得意な方も苦手な方も 三平方定理の問題の解き方を教えてください。 三平方定理の問題が出たのですがサッパリ分かりません。三平方の定理アニメーション 求積による求積法の表現、最大和、最小和、左端和,右端和,台形公式、シンプソンの公式 定積分と積分法の基本定理の視覚化と平均値の定理の視覚化 上付文字、下付文字、分数、ルート、ベクトル記号の表示も可能です。




三角比 30 45 60 もう一度やり直しの算数 数学




三平方の定理の証明と使い方
一方、3、4、5のような三平方の関係を満足する整数の組をピタゴラス数という。mとnを正の整数とすると(m>n)、 m 2 -n 2, 2mn, m 2 +n 2 はピタゴラス数になる。三平方の定理は平面や空間の2点間の距離の公式の基礎でもある。 柴田敏男ヘロンの公式 計算機 使い方! 入力値は、整数・分数・小数のいずれか、当然ですが正の値に限ります。 入力可能文字数(桁数ではありません)は、最大7文字です。 (「12/5」は4文字、「」は6文字とカウントされます) 「1/2」(2分の1)のように三平方の定理( さんへいほうのていり ) 、 勾股弦の定理( こうこげんのていり ) とも呼ばれる。 ピタゴラスの定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。




三角比6 三平方の定理の暗算 怜悧玲瓏 高校数学を天空から俯瞰する
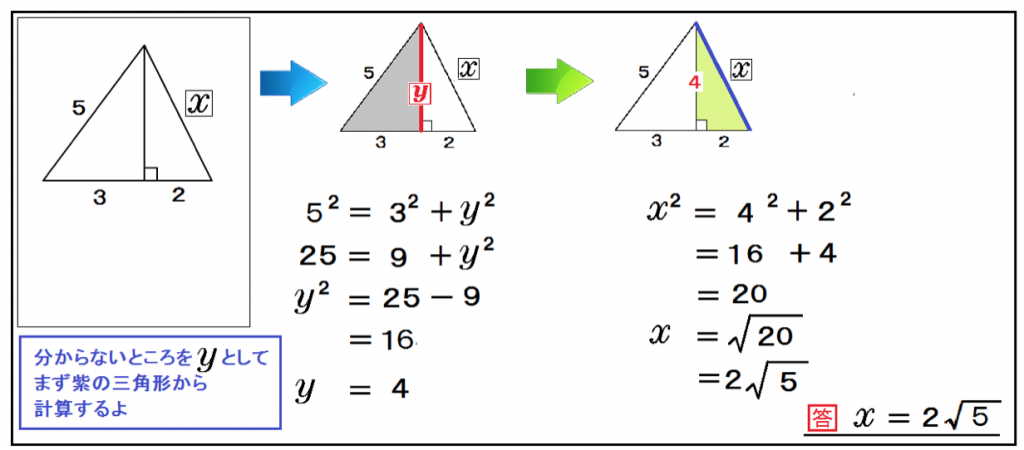



三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく
平方根 (分母の有理化) 中3数学 分数の上下に同じ数字を掛けて、分母のルートを外す作業です。 ルートの計算がしっかり定着していれば決して難しくはないですが、約分やルートを簡単にできるときは必ずすることだけは注意しましょう。




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



Studydoctor三平方の定理の利用 中学3年数学 Studydoctor




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく
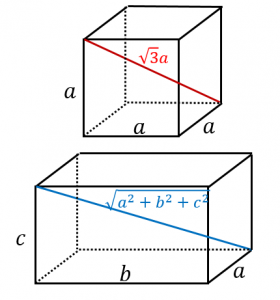



立方体と直方体の対角線の長さ 具体例で学ぶ数学
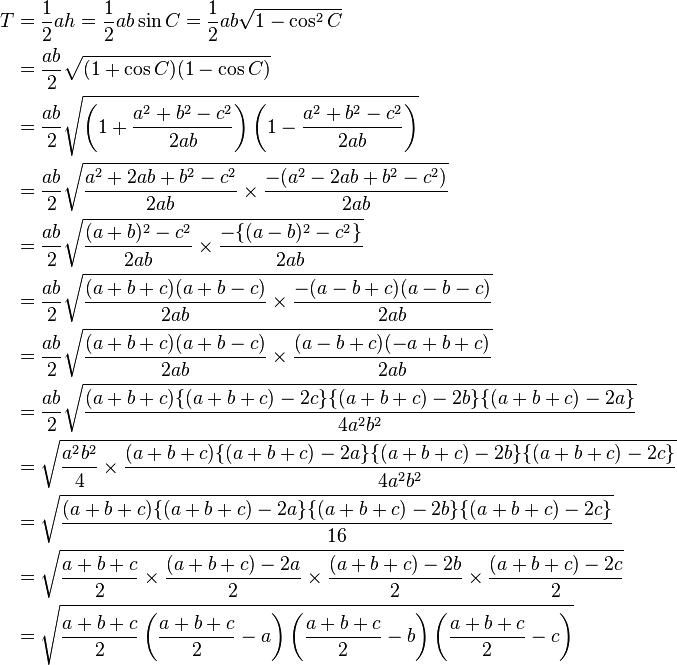



ヘロンの公式の証明 三角関数を使わずに ようこそ なるのホームページへ
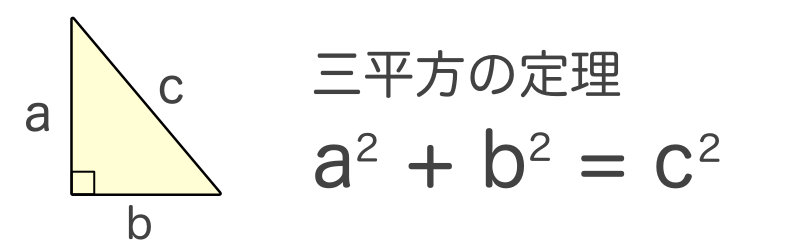



三平方の定理 簡単に計算できる電卓サイト




1 2 ルート3の三角形




上の囲んでいる三角形のacの辺を求めるのが下の囲んでいる式なのですが 高校 教えて Goo




わかりやすい三角比と基本公式 Irohabook



受験 定期試験 数学解き方集 裏技 解法 三平方の定理のテクニック 中学数学 高校数学




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




ウケる数学 三平方の定理で解く 地平線までの距離 中日新聞web




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




直角三角形の辺の長さ 合同条件 面積について アタリマエ




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



ピタゴラスの定理 Wikipedia



1




1 2 ルート3



の由来 Fukusukeの数学めも




三平方の定理と二等辺三角形 Youtube



1




三平方の定理の計算工夫 勉強を頑張っている人のための勉強法



三平方の定理
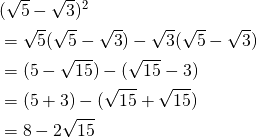



ルート 根号 の計算方法をマスターしよう スタディクラブ情報局
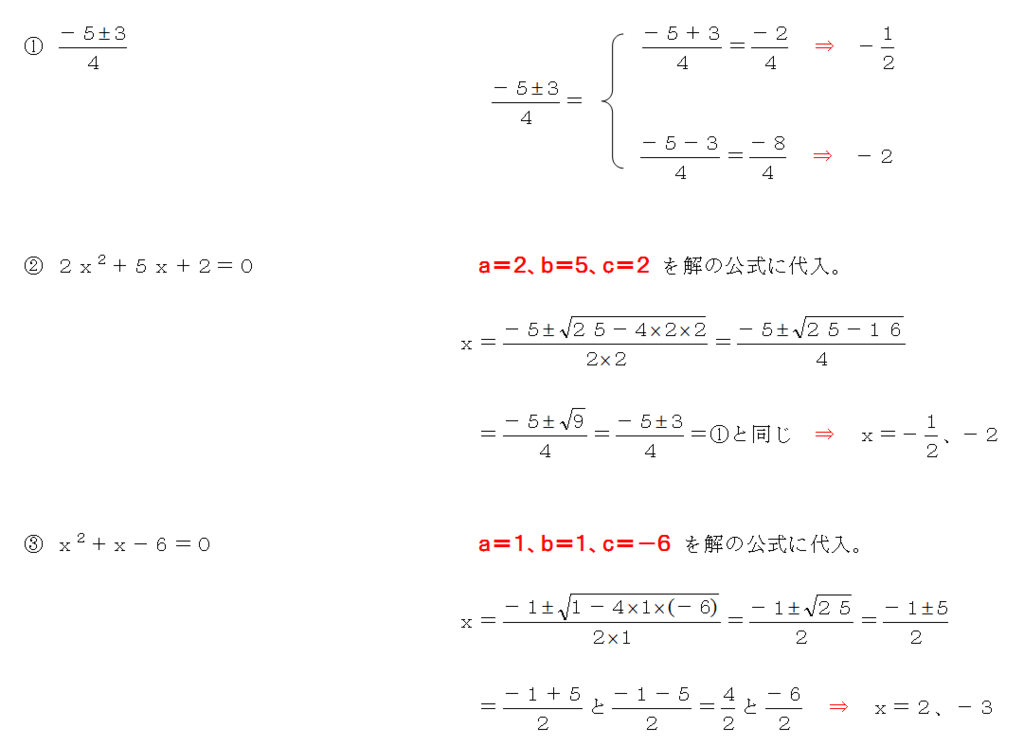



解の公式を使う問題 答えがルートにならないパターン 中学や高校の数学の計算問題




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




中学数学 直角三角形の辺の長さの求め方 超丁寧に なぜか分かる はかせちゃんの怪しい研究室




三平方の定理で3 4 5を習ってないのですが 簡潔に説明お願いします Clear




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座
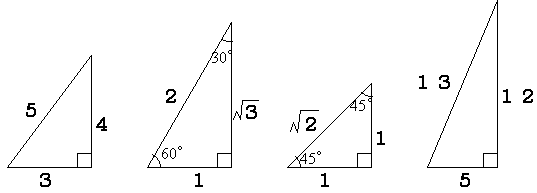



三角形の性質




三平方の定理 自動計算サイト



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




中3数学 2点間の距離 の公式とは 映像授業のtry It トライイット




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題




三平方の定理 覚えておきたい基本公式を解説 数スタ



1




問題49の解説で B座標がなぜ マイナスルート2a 2a2乗 と分かるのでしょうか Clear




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学




ルート5ほかの近似値 三平方の定理 よし坊のブログ



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




なぜ3の2乗 6の2乗の上にルートを付けなければならないのですか Clear




三平方の定理で ルートがつく計算になるのはなぜですか Clear




ルート 根号 の計算方法をマスターしよう スタディクラブ情報局




21番はなぜ三平方の定理にルートがはいってるのですか Clear



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




受験数学 三平方の定理で1 1 ルート2は使えなくても大丈夫だぞ 中学数学 福岡県 小郡市の個別指導専門の学習塾 志義ゼミナール




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく
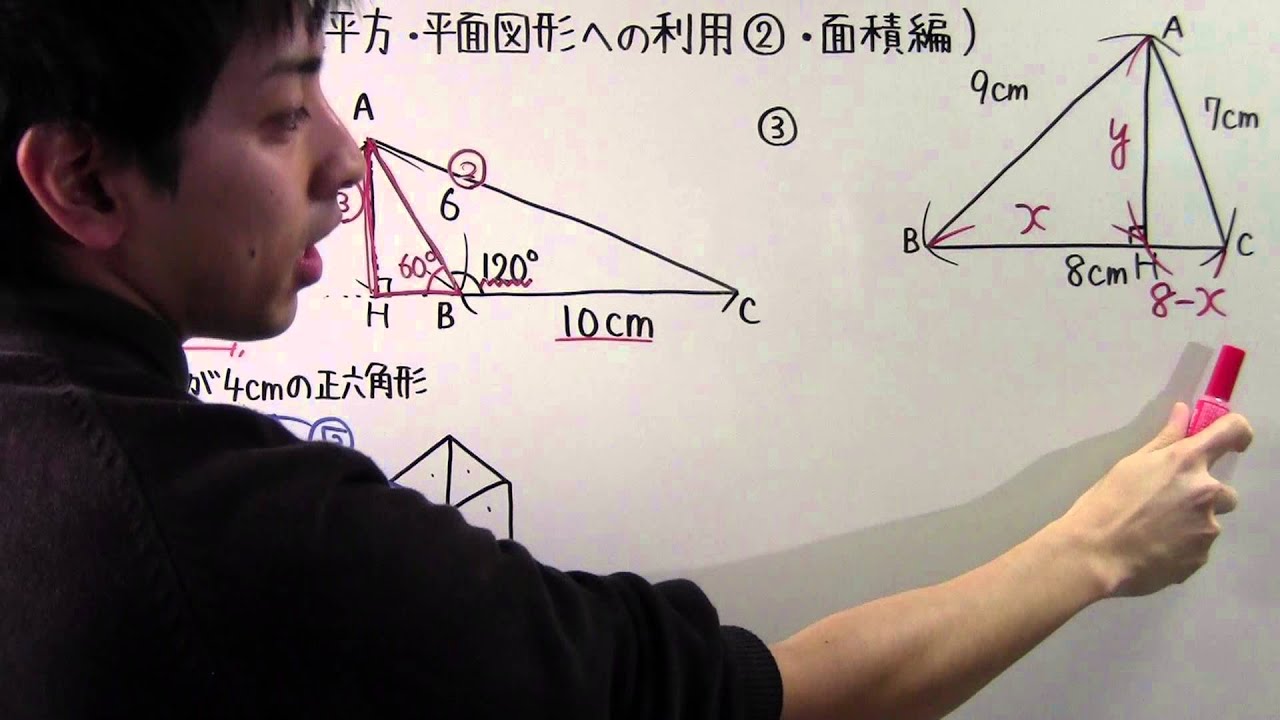



数学 中3 64 三平方 平面図形への利用 面積編 Youtube




受験数学 三平方の定理で1 2 ルート3は使えなくても大丈夫だぞ 中学数学 福岡県 小郡市の個別指導専門の学習塾 志義ゼミナール
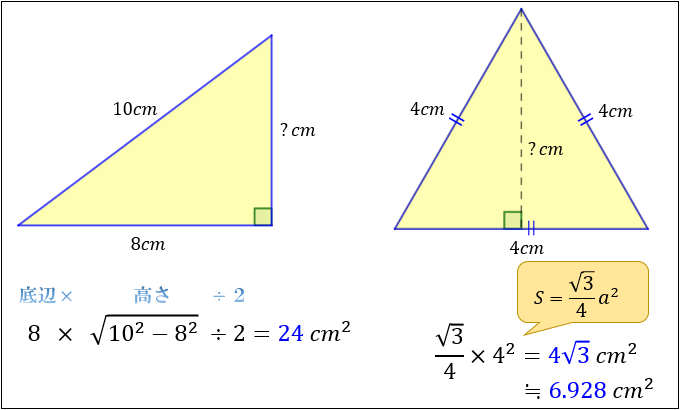



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




平面図形37 平方根の作図 怜悧玲瓏 高校数学を天空から俯瞰する




三平方の定理で辺を求める Youtube




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




数学 中3 63 三平方 平面図形への利用 基本編 Youtube




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



直角三角形の1 2 ルート3という公式はなぜ成立するんですか 1 1 ルート2 Yahoo 知恵袋
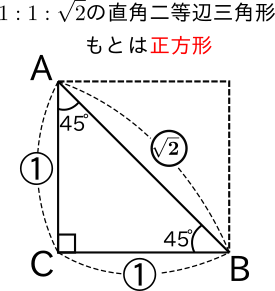



受験数学 三平方の定理で1 1 ルート2は使えなくても大丈夫だぞ 中学数学 福岡県 小郡市の個別指導専門の学習塾 志義ゼミナール
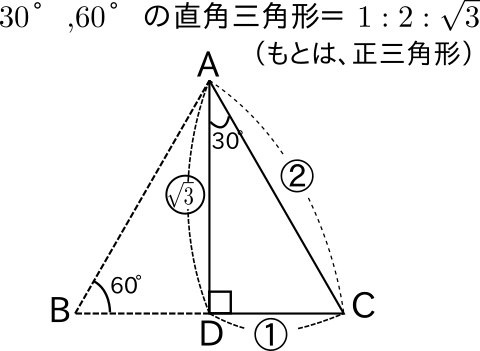



受験数学 三平方の定理で1 2 ルート3は使えなくても大丈夫だぞ 中学数学 福岡県 小郡市の個別指導専門の学習塾 志義ゼミナール




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく
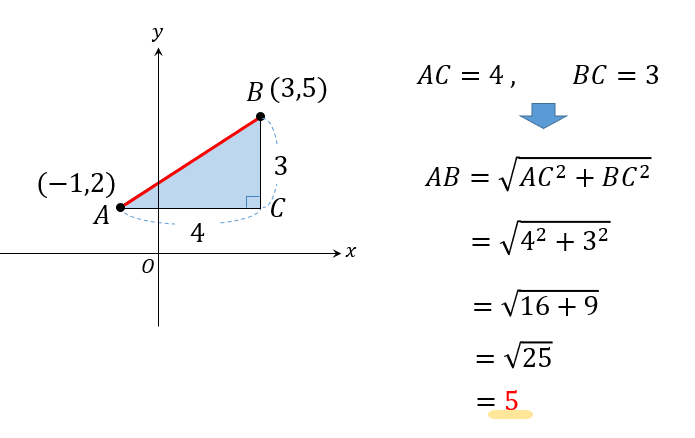



中学数学 二点間の距離の求め方をイチから解説 数スタ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
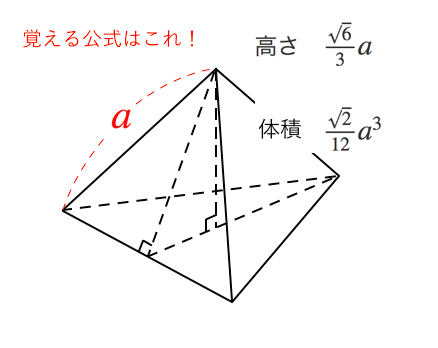



正四面体 高さ 面積を求める公式 苦手な数学を簡単に




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導



かなり難しい中学受験の算数の問題です 問題文と図は写真の通り Yahoo 知恵袋
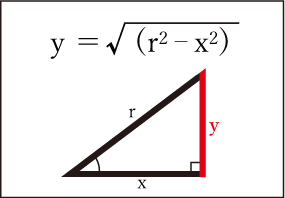



三角関数をマスターしよう その3 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習
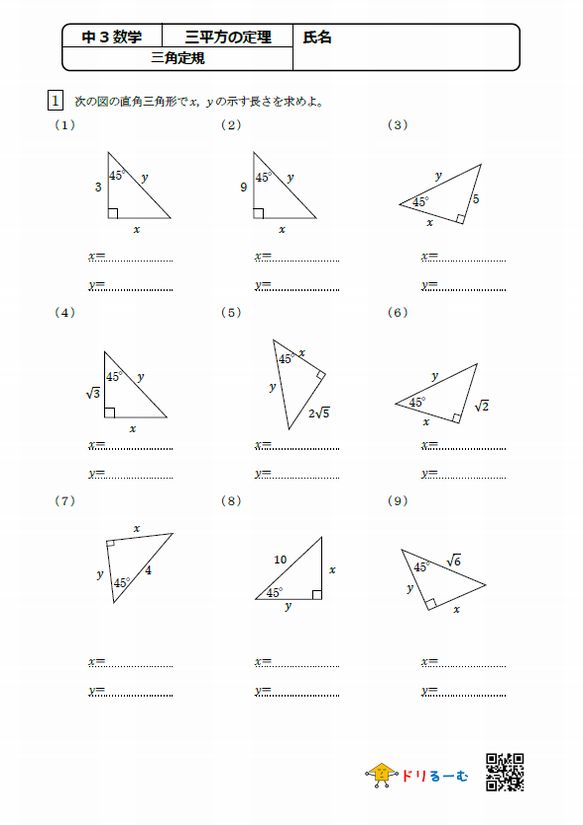



三角定規 ドリるーむ
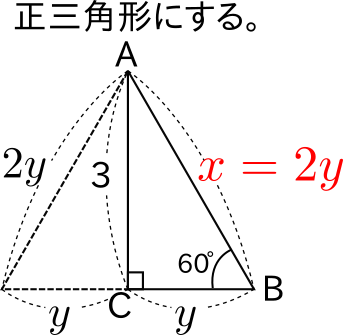



受験数学 三平方の定理で1 2 ルート3は使えなくても大丈夫だぞ 中学数学 福岡県 小郡市の個別指導専門の学習塾 志義ゼミナール




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ
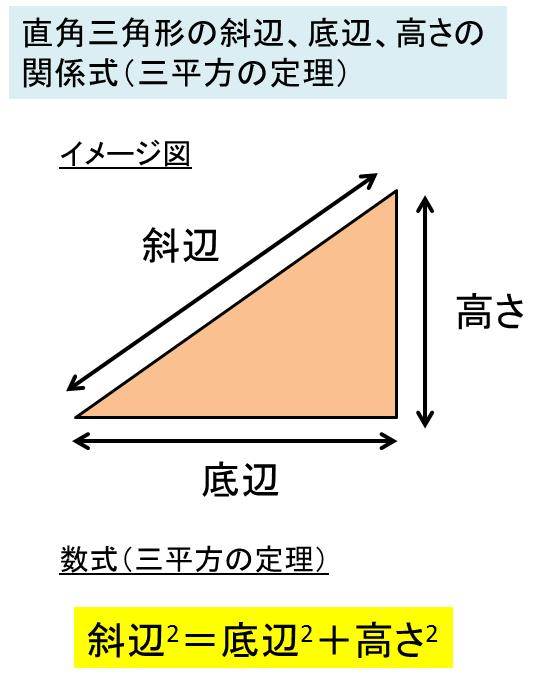



Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



三平方の定理の公式で 直角二等辺三角形は1 1 ルート2という Yahoo 知恵袋




答えはルート3です教えてください Clear




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook




三平方の定理の応用




数学 中3 61 三平方の定理 基本編 Youtube




二次方程式の解き方 平方根の知識を使う問題のパターン 中学や高校の数学の計算問題



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス



ピタゴラスの定理 一級建築士の型枠大工 北村工業



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




1 1 ルート2 三角形



ピタゴラスの定理 三角関数 ルート計算方法 小池啓仁 ヒロヒト応援ブログ By はてな




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



1



0 件のコメント:
コメントを投稿